Statistiques et probabilités
Quel est la définition d'une statistique ?
Ensemble de données d'observation relatives à un groupe d'individus ou d'unités (souvent pluriel). 2. Ensemble des méthodes qui ont pour objet la collecte, le traitement et l'interprétation de ces données.
Quel est le but de la statistique ?
Le but de la statistique est d'extraire des informations pertinentes d'une liste de nombres difficile à interpréter par une simple lecture. Deux grandes familles de méthodes sont utilisées selon les circonstances.
Quel est le rôle de la statistique ?
Les statistiques servent à réduire les gros nombres à une dimension où it est plus facile de les comprendre. Les hommes aiment recueillir des chiffres, à les combiner de diverses façons, ì en tirer des conclusions et à les citer.
Quel est le but et l'objectif de la statistique ?
La statistique a pour but d'étudier les faits pour permettre ensuite de prendre des décisions. On conçoit alors qu'elle puisse être dangereuse si l'étude a été viciée par des erreurs d'observation, ou par des erreurs d'interprétation.
Pourquoi on fait une étude statistique ?
Tout d'abord, pourquoi faire des tests statistiques ? Les tests statistiques (ou tests d'hypothèses) vont vous permettre de tirer des conclusions claires, mathématiquement rigoureuses (et élégantes !) à partir des données que vous aurez analysées.
Primaire - sixième
- Traitements des données
- Calcul des moyennes
A partir de 10€/h
Secondaires
-
La statistique descriptive à une variable
- Moyenne
- Effectif
- Etendue
- Mode
- Classe
- Ecart-type
- etc...
A partir de 15€/h
Supérieurs - baschelier
- Lois de probabilité
- Lois statistiques
- Tests d'hypothèses
- etc...
A partir de 20€/h
Quelles sont les lois de probabilité ?
Elle comporte les lois binomiale, Poisson, binomiale négative, Gamma, normale et une sixième sans nom propre. Elles ont pour propriété que la somme de deux variables indépendantes a une distribution de même forme (appelée la convolution).
Quand utiliser la loi normale et la loi de Student ?
Le test de Student est un outil permettant de vérifier une hypothèse formulée sur un jeu de données. Il est principalement utilisé lorsque l'on sait que l'échantillon de données est supposé suivre une loi normale, comme lorsque l'on joue 100 fois de suite au pile ou face.
Quelle est la loi de distribution la plus utilisée en statistique ?
La loi normale est la loi statistique la plus répandue et la plus utile.
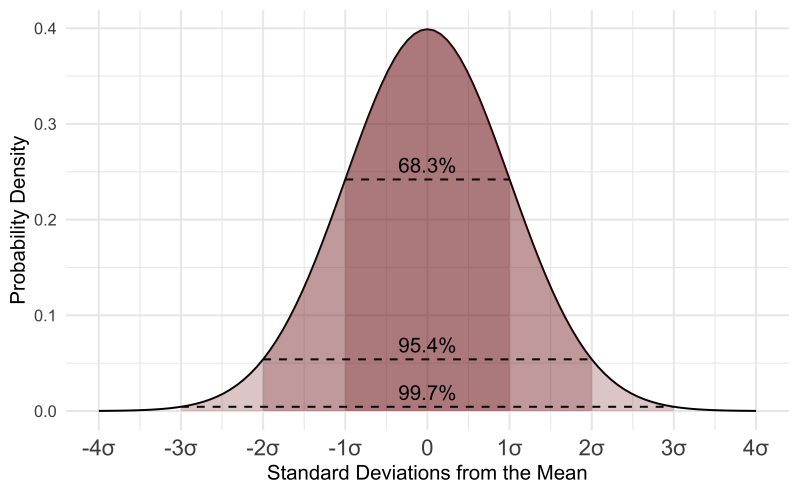
La courbe de Gauss, ou courbe de la loi normale ou encore courbe en cloche, permet une représentation graphique de la distribution d'une série. Elle permet tout particulièrement de représenter la densité de mesure d'une série statistique.

Comment utiliser la loi du Khi-deux ?
Le test du chi-carré est un moyen statistique de déterminer les différences entre ce qui était attendu et ce qui a été observé dans une ou plusieurs catégories. Les chercheurs utilisent ce test non paramétrique pour comparer des variables catégorielles au sein d'un même échantillon de population.
La loi du χ2 intervient de la façon suivante : si X1,…,Xn X 1 , … , X n sont n variables aléatoires qui suivent une loi normale centrée réduite, alors la somme de leur carré X21+⋯+X2n X 1 2 + ⋯ + X n 2 suit une loi du χ2 à n degrés de liberté. Cette propriété fonde les test statistiques du χ2. χ 2 .

Quand on utilise la loi de Poisson ?
Discrète mais bien connue, la loi de Poisson est une loi de probabilité qui s'applique aux évènements rares. Parmi ses domaines de prédilection, les contrôles de qualité (y compris révision comptable, puisqu'on suppose que les erreurs sont rares), les probabilités de défaut de crédit, les accidents...

Pourquoi utiliser la loi binomial ?
En probabilité, la loi binomiale permet de décrire le nombre de succès dans une série d'expériences identiques et indépendantes, où il existe deux résultats possibles : succès ou échec. Elle est définie par deux paramètres : le nombre total d'expériences (n) et la probabilité de succès dans chaque expérience (p).
Quand utiliser la loi de Weibull ?
La distribution de Weibull est souvent utilisée dans le domaine de l'analyse de la durée de vie, grâce à sa flexibilité : comme dit précédemment, elle permet de représenter au moins approximativement une infinité de lois de probabilité. Articles détaillés : Loi de fiabilité et Analyse de survie.

Quand on utilise le test de Fisher ?
Lorsque l'un des effectifs théoriques est inférieur à 5 ou lorsque les sommes marginales du jeu de données réel sont très déséquilibrées, il est préférable de se fier au test exact de Fisher.
Tests d'hypothèses
En statistiques, un test, ou test d'hypothèse, est une procédure de décision entre deux hypothèses. Il s'agit d'une démarche consistant à rejeter ou à ne pas rejeter une hypothèse statistique, appelée hypothèse nulle, en fonction d'un échantillon de données.
Comment réaliser un test d'hypothèse ?
La construction d'un test d'hypothèse consiste en fait à déterminer entre quelles valeurs peut varier la variable aléatoire, en supposant l'hypothèse vraie, sur la seule considération du hasard de l'échantillonnage.
Quelle est l'hypothèse nulle H0 ?
L'hypothèse nulle notée H0 est l'hypothèse que l'on désire contrôler : elle consiste à dire qu'il n'existe pas de différence entre les paramètres comparés ou que la différence observée n'est pas significative et est due aux fluctuations d'échantillonnage. Cette hypothèse est formulée dans le but d'être rejetée.
Comment définir H0 et H1 ?
Cela s'articule habituellement autour de l'hypothèse nulle (H0): si on accepte l'hypothèse nulle, l'hypothèse alternative (H1) est infirmée; inversement, si on rejette l'hypothèse nulle, l'hypothèse alternative est confirmée.
Quand on rejette H0 ?
Pour prendre une décision, choisissez le niveau de significativité α (alpha), avant le test : Si p est inférieur ou égal à α, rejetez H0. Si p est supérieur à α, ne rejetez pas H0 (en principe, vous n'acceptez jamais l'hypothèse H0, mais vous vous contentez de ne pas la rejeter)


Créez votre propre site internet avec Webador